
向上!我們怎麼知道「上」是指哪裡呢?因為我們是立體國的人,我們是在一個有三個維度的空間生活。但是對於平面國的人來說,「向上」他們不知道哪裡是「上」,反而會以為是要「往北」,這就是本書有趣的地方:說明了不同國家、不同世界的人對於觀念理解的歧異性,主軸雖然在於說明各種幾何圖形,然而在過程中也透過幾何圖形說明了社會的問題。
主角是個正方形,而平面國裡有各種形狀的人,三角形、等腰三角形、正三角形、五角形、六角形等等等等直到圓形。當然,圓形可能只是趨近於無限的邊所組成的接近圓弧的形狀,然而「邊」這件事情在平面國中代表的正是階級,邊數越多,越是崇高。然而無論是什麼形狀,對於任何平面國民來說他們看到的都是「一條直線」,這就像我們放一個東西在桌面上,然後我們把視線切齊桌面所將會看到的東西,在平面的世界裡用遠都會是一條直線,只在立體國度我們才能分辨形狀的差別。
《平面國》是主角的回憶錄,那他之所以寫出這本回憶錄是因為他被「球體」給啟蒙了,試想在一個平面上看到的球體會是什麼?一個圓形。當然,平面國民是看不到圓形的,他們的「視覺辨認」技術在於前後兩邊距離遠近造成的亮度變化,這是平面國最高級的辨認技術,甚至在上流社會中用下級的「觸摸辨認」是一種失禮的行為。回過頭來,這個球體在千禧年出現在正方形的世界中,告訴正方形他在立體世界中俯瞰平面國可以知道的所有事情;但正方形不相信,就算球體「從上往下」拿走了櫃子中的帳簿,這還是太超常了。直到球體帶正方形進入立體國的世界才讓他眼界大開,若一個點的延伸會成為一條線,一條線的平面移動將會出現一個平面,那麼一個平面的向上移動就會出現一個物體了,這是推論可以達成的,但若無前提認知時,怎麼可能知道「向上」是什麼意思呢?
與球體的第三類接觸是《平面國》後半段的主軸,說明了知識也是信念的一種,如同在《沒有神的宗教》中德沃金指出了知識也是網狀的交互支撐,也就是說沒有一個根本的基礎能推論出所有現存的知識,而是相互證成彼此。那麼當球體出現在平面國出現時基本上可以認為是一個「異例」,但在舊有範疇中的所有形狀都無法處理這些問題,是直到範疇的更易才讓理解這種新穎現象成為可能,而這個更易過程正是孔恩所說的典範轉移(Paradigm shift)。
不過有趣的事情是,近似於神的存在的球體,也受限於自身的範疇。當正方形以同樣的推理方式推論出如果點到平面到空間是分別依照等比數列與等差數列增長時,那麼從一維到二維到三維不應該是全部,而應該還有四維到五維到六維,甚至更多更多,但球體面臨這個邏輯正確但經驗無法證明的命題時卻強烈否認。這樣的反應在生活經驗中並不陌生,我想這說明了即便我們認為是神的存在或許不過是個誤會,因為這樣的個體也不過跟差了一個「維度」的個體一樣有著瑕疵,也會否認真理。
當然,球體傳遞這些知識給正方形並非一無所求,他希望正方形成為知識的傳教士,讓所有平面國的人知道立體國的存在,但實際上平面國的菁英早就知道這些事情了。每逢千禧年,球體都會拜訪平面國,但也是在這個時期,圓形的菁英階級徹底封禁主張立體國存在的言論。正方形對於真理與知識的熱忱讓他不得不說出真相,但也使得他必須在獄中寫出這本回憶錄。
如同方才所述,平面國是依照邊的數量來區分階級的,士兵和勞工通稱是等腰三角形,等邊11英吋(約28公分),底邊半英寸(1.27公分),越是下等越是尖銳,專業人士和仕紳是正方形與五邊形,而越是往上的邊則是越多,直到祭司。在這樣的秩序中另有一個自然法則,就是子嗣會比上一代多一條邊,階級代代提升,但這個規則不適用於商人、士兵與工人。等腰三角後代依然是等腰三角,除非他們十分努力或功勳彪炳,再經過聯姻才可能生出「正三角形」,雖然要官方認證,雖然確認後馬上要送到無子的正三角家庭而不得再與原生家庭接觸。但對於圓形(多邊形)的自然法則則不同,在這裡,階級提升之後,提升速度會越來越快,但同時繁衍會更困難,他們很難有子嗣,但如果有子嗣可能是從四百五十邊形跳躍成五百五十邊形。但無論是什麼階級,對於爬升階級是沒有區別的,就連在多邊形階級中,把剛生下的柔軟小孩折半再折半,這樣邊數就更多了,雖然存活率只有十分之一,但是他們還是前仆後繼。
而這樣的階級秩序也是平面國中的教條:「改進您的形狀。」無論是任何領域,政治也好、宗教或道德,一切都是為了提升形狀,最後達到圓形,個人的意志、努力、訓練或是各種德行,全部被否定,所有的功勞或過錯都是形狀所致,無論這是先天而來或是跟人群碰撞所造成,這樣的決定論成為平面國的共識。沒有任何形狀具有能動性,若生下來是正方形,那麼正方形的人生路線就已經被決定了,就算沒有完全決定,也會在環境中與人的碰撞中被決定,但無論如何個體的將來都與他自身的意志所做出的決定無關。這個階級秩序是如此僵固,僵固得所有人信守這個模式而無法跳脫,唯一的可能性或許也只剩下千禧年的球體神啟了。
而到目前為止所說的是依照邊數所做的區分,但除了邊數之外,形狀的「規則」與否更是具有決定性的,在這裡,「不規則」等同於道德瑕疵,對待不規則形狀可以如同對待罪犯一般?他們或許也活得很辛苦,但平面國中所有人的利益比起一個畸形而言,是更為被優先考量的東西。

在平面國民的認知中,不規則形狀有誘騙的能力,而且他們難以抗拒欺騙他人。「因此,對於這群人,我們絕對要群起而攻之!讓那些虛假的善心人士繼續去嚷嚷著廢除對不規則形狀的不平等法律吧!就我個人而言,我從來沒看過哪一片不規則形狀的人不虛偽、不離群所居、不盡其所能地為非作歹,大自然讓他們生成這副模樣真的是用心良苦。」但正方形還是有著慈悲心,他認為醫療技術的進步以及飲食得控制,都可以改善不規則的形狀讓他們有機會變成「正」的:「因此,透過這本書,我在此向諸位昭告我個人的想法,對於剛剛出生的不規則多邊形,我認為並不應該制定絕對的衡量標準,但當醫療團隊宣布無法將他們調整為正多邊形時,我便建議將這些不規則多邊形嬰孩們,全數仁慈地、無痛苦地、殺掉。」
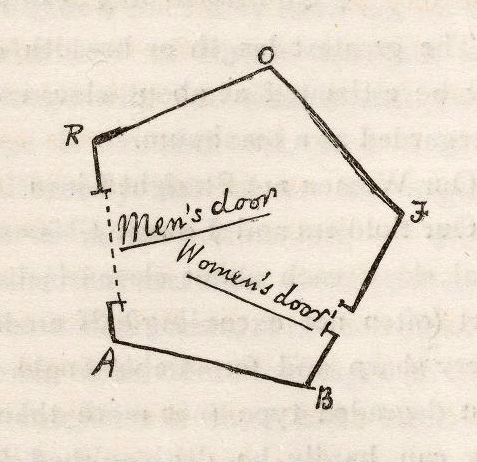
到這裡還沒提到另一個最大的族群,也就是女性,女性的形狀是直線,沒有任何其他的可能性,她們的形狀類似於男性中最卑下的階級,但不同的是,等腰三角形的男性有機會努力增加角度而產生階級流動,但女性則是被大自然裁決:「生為女人,一生為女人。」然而同時,大自然讓女性不活得那麼痛苦的方式是剝奪她們回憶與思考的能力,避免她們意識到生存慘狀才能活下去。而平面國也因應著女性的樣貌去制定法規,例如女性因為是一根針隨時會刺穿別人太過於危險,所以只能從房子中專屬女性的小門進出,行走時還必須不斷地出聲提醒他人自己的存在否則將面臨死刑。男性因為有形狀而得以被辨識,但因女性都是直線所以政府會留下所有的族譜以確定該女性有無潛在的不規則特質。女性也因為被認為無法理性思考,被排拒在教育制度之外,一代一代的退化。
看完平面國中正方形的自傳,與我們所生活的地方其實相差不遠:對於異常者的迫害,無論是種族、信仰還是精神疾病;認為女性天生卑劣甚至在制度上予以壓迫;或是在本書中提到的圓形階級對於彩繪革命(也就是低下階層發想而出透過彩繪各種形狀辨識出圖形以產生階級顛覆)的反動打壓。寓言般的故事讓我們不得不去檢視自己的周遭:我們不也是這樣嗎?知識上的突破成為對現有秩序的威脅,階級利益優於知識與進步的考量;在台灣的語境中,最重要的是「規則與不規則」的問題,原則上我們可以認為在《平面國》這本書中是「自然性」的東西,若將其性質轉化為「文化性」的,也就是說讓「維度成為文化的」,那就能成為認知我們社會的工具了。
不規則的人,例如外在的畸形或是精神上的疾病,被認定就是天生邪惡就是愛做錯事,光是有這個「不規則」的特徵出現,我們就可以用對待罪犯的方式來對待他們,正方形說出了平民的道德感情,而當道德感情凝聚也將成為民粹的湧流。一旦發生精神疾病患者殺人案件,精神病這個「不規則特徵」總是被特意放大,但若實際比較「有精神疾病」與「無精神疾病」的殺人比例,前者會比後者高嗎?絕對不會。那麼是出於什麼原因這個特徵被放大且渲染呢?除了媒體的點閱率與觀看次數的業績追求之外,或許也因為在這種方式下可以讓人民產生共鳴。然而,對於不該是敵人的個體將其定性為敵人,進而對他發起戰爭,這是我們要的公民社會嗎?如果我們看到《平面國》的歷史、規定以及現狀覺得荒謬好笑,那我們如果有一天能到文化上的第四維度來看我們現處的文化上的三維空間,我們可能也會覺得自己離譜得可悲。
書籍資訊
書名:《平面國:向上而非向北》 Flatland: A Romance of Many Dimensions
作者: 愛德溫‧A‧艾勃特(Edwin Abbott Abbott)
出版:木馬文化
日期:2019











 最新文章
最新文章 主題總覽
主題總覽 成為粉絲
成為粉絲 追蹤IG
追蹤IG 追蹤推特
追蹤推特 也有串串
也有串串 合作提案
合作提案