
文|Steven Pinker
譯|陳岳辰
人類給未知事件安上數字,就能量化自己對未來的判斷。預測是一門深奧的學問,影響政策、投資、風險管理,也涉及平日對生活的規畫。試想下面列出的事件,寫下你認為未來十年內成真的機率。其中許多事很難成真,所以我們的量尺末端刻度做精細一點,然後分出幾個等級:低於千分之一、千分之一、千分之五、百分之一、百分之二、百分之五、百分之十、百分之二十五、百分之五十以上。
● 沙烏地阿拉伯發展核武。
● 尼古拉斯.馬杜洛(Nicolas Maduro)辭去委內瑞拉總統職位。
● 俄羅斯出現女總統。
● 比新冠肺炎更致命的傳染病在全球大流行。
● 俄羅斯修憲,規定普丁不得再次參選總統,但他的妻子贏得大選,實際上大權仍掌握在他手中。
● 尼古拉斯.馬杜洛因為激烈的罷工和抗爭被迫辭去委內瑞拉總統。
● 中國境內呼吸道病毒從蝙蝠轉移到人類身上,於是引發比新冠肺炎更致命的流行病。
● 伊朗發展核武並進行地下試爆,沙烏地阿拉伯為自保也開始發展核武。
我在某次調查裡對數百位受試者提出類似問題,整理問卷之後發現有趣的現象:大家認為普丁妻子成為俄羅斯總統的機率比俄羅斯出現女總統的機率高,馬杜洛因為罷工抗爭下臺的機率比馬杜洛下臺的機率高,沙烏地阿拉伯因應伊朗威脅發展核武比沙烏地阿拉伯發展核武的機率高,中國蝙蝠造成新疫情的機率比地球出現新疫情的機率高。
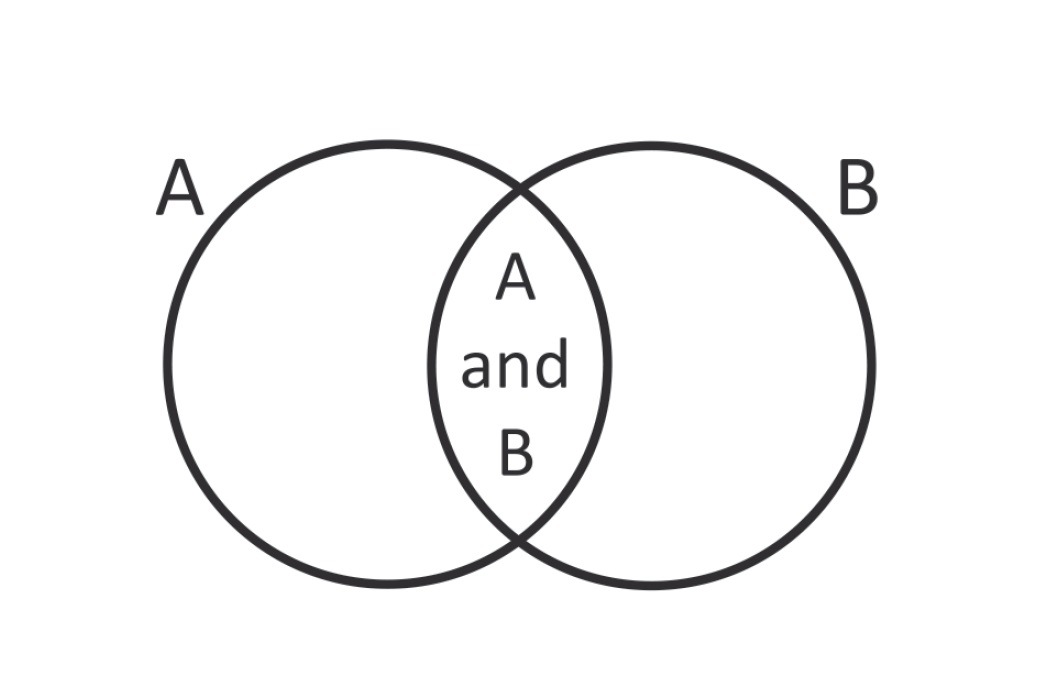
現在讀著本書的你或許也同意其中至少一個對比句,因為問卷結果顯示,認同一句以上的人多達百分之八十六。如此一來你就違反了機率的基礎,也就是交集原則:複數事件(A及B)的交集機率必須小於或等於單一事件(A,或B)的機率。譬如從撲克牌中抽到偶數黑桃的機率一定比單純抽到黑桃的機率來得低,因為黑桃不只有偶數,還有奇數。
前面八個事件兩兩一組形成四句陳述,每句話的前半是交集,後半是被交集的事件。比方說「沙烏地阿拉伯因應伊朗威脅發展核武」是交集,「沙烏地阿拉伯發展核武」是被交集的事件,後者機率一定比前者高,因為沙烏地阿拉伯有可能基於別的理由發展核武(對抗以色列、想拿下波斯灣主導權等等)。同樣邏輯,罷工抗爭可以逼迫馬杜洛下臺,但他也可能因為別的理由下臺。
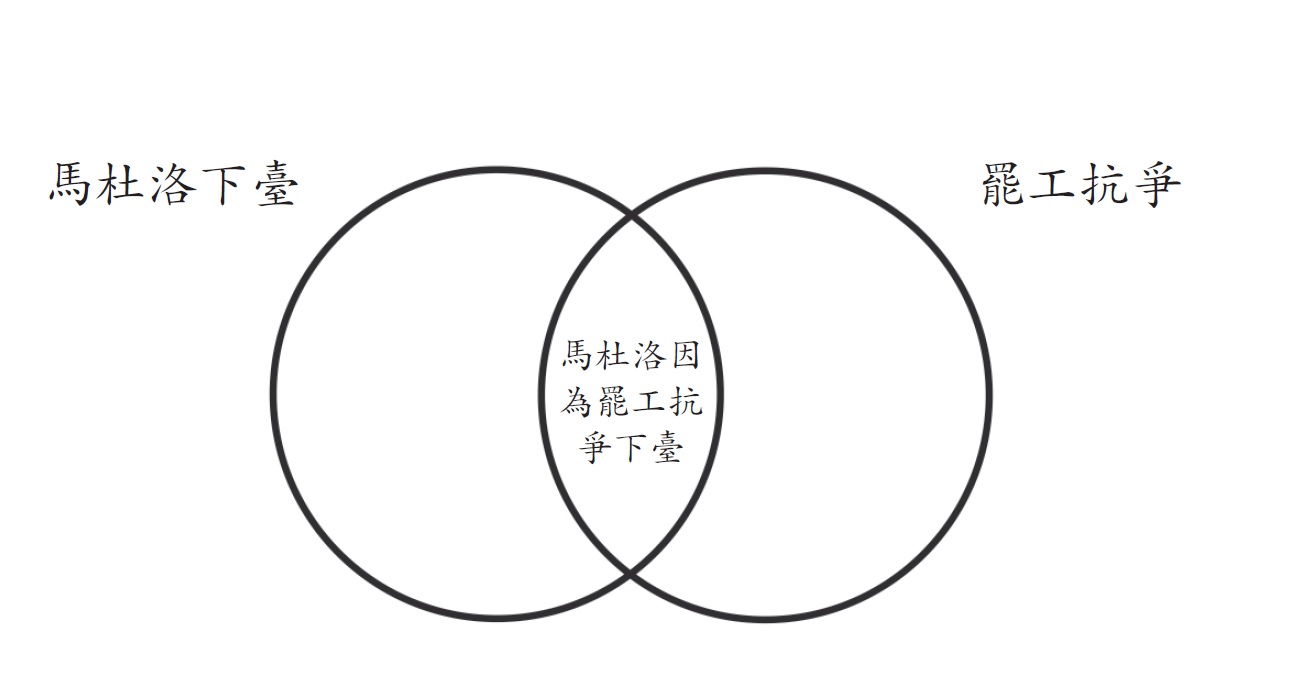
為什麼很多人弄反?因為每組裡的後半句話抽象空泛,人類心智較難掌握意義。作為交集的前半句話不僅脈絡明確,還拼湊得出故事劇情,大腦很容易轉換為具體畫面。如果交給直覺判斷,越容易想像的事情感覺機率越高,越清晰的畫面感覺越可能成真。換句話說,我們一不小心就會認為交集的發生機率大於被交集的元素,康納曼和特沃斯基稱之為「合取謬誤」(conjunction fallacy)。
所謂的「名嘴」常以生動描述發表預測,才不管什麼機率問題。《大西洋》月刊(The Atlantic)一九九四年採用記者羅伯特.卡普蘭(Robert Kaplan)的專文報導作為封面故事,標題為「即將到來的無政府狀態」(The Coming Anarchy),他預測二十一世紀第一個十年人類會為了爭奪包括水在內的稀缺資源陷入戰亂,奈及利亞攻下尼日、貝南和喀麥隆,以非洲為起點的戰火襲捲世界,導致美國、加拿大、印度、中國、奈及利亞分崩離析,拉丁美洲各國與墨西哥之間不再有國界,加拿大亞伯達省與美國蒙大拿州合併,美國大城市犯罪率節節飆升,愛滋病人口不減反增,同時還會遭遇十數種大型天災人禍。文章非常轟動(連當時的美國總統柯林頓都叫白宮官員仔細讀),但現實世界裡各國內戰逐漸減少,無法取得乾淨水源的人口下降,美國犯罪率屢創新低。距離文章發表不到三年,新的愛滋病療法有效延長了患者壽命,各國疆界超過二十五年動也不動。
特沃斯基和康納曼解釋何謂合取謬誤時舉了一個例子,後來成為有名的「琳達問題」:
琳達三十一歲,單身,說話直接,腦袋機伶。大學主修哲學,學生時代相當關注歧視和社會正義議題,曾經參與反核遊行。請分析下列陳述的可能性。
● 琳達在小學任教
● 琳達積極參與女權運動
● 琳達是精神醫療社工
● 琳達是銀行行員
● 琳達是保險業務員
● 琳達是積極參與女權運動的銀行行員
許多作答者認為琳達是女權主義者銀行行員的機率比起她只是單純銀行行員還要高。同樣地,A及B同時成立的機率被估得比只有A成立還要高。這個題目放到現在稍微過氣了,因為「琳達」是嬰兒潮世代常見的名字,「機伶」看似正面其實略帶挖苦,而那些抗議也是過去的事情,連提到的行業都已經不大流行,整體散發出濃濃的二十世紀風味。不過對心理學家來說同樣效果很容易複製,只要換成高智商的阿曼達曾經參與過「黑人的命也是命」運動,依舊很多人認為她比較有可能是關注女權的有照護理師,卻比較不可能是單純的有照護理師。
琳達問題從一個特別刁鑽的角度考驗人類直覺。先前提到的幾種選擇問題,大家做錯是因為題目太抽象(「若P則Q」),改成貼近真實生活的場景反而能答對。現在反過來了,抽象法則「[A及B同時成立的機率]小於或等於[A成立的機率]」是所有人的共識,然而具體描述情境之後很多人卻推翻了法則。生物學家兼科普作家史蒂芬.傑伊.古爾德(Stephen Jay Gould)代表很多人說出心聲:「我其實知道那句(合取)陳述可能性比較低,但是好像有個小人兒在腦袋裡跳上跳下大吼大叫說:『她怎麼可能只是個普通銀行行員,前面都說了那麼多關於她的事情。』」
高明的說客懂得如何喚醒別人腦袋裡那個小人兒。檢察官手邊證據只有沖上海岸的屍體,於是開始假設是丈夫悶死太太後棄屍,詐領保險理賠以後與外遇對象遠走高飛。辯方律師也會編故事,說死者很可能是深夜碰上搶匪,衝突中鬧出人命。其實根據機率原則,劇本加入越多細節可能性就越低,但同時又更能打動人。戲劇《天皇》(The Mikado)裡面普巴(Pooh-Bah)的臺詞有一句是:「原本荒誕無稽的說法,只要加進活靈活現的描述,就能增加藝術上的可信度。」
合取原則應該是計算機率時的數學基礎,而且不需要代入數字也能理解。正因如此,特沃斯基和康納曼對人類的機率直覺抱持悲觀態度,典型的刻板印象與可得的記憶左右了大腦,系統性評估反而被擠到思維之外。俗話說:「每個瘋子身體裡都有個清醒的人想逃出來。」但他們認為那個清醒的人根本不存在。
其他心理學家沒這麼絕望。前面解釋蒙提.霍爾選擇時提到過,「機率」其實有好幾層意義,包括物理上的傾向、信念的證據強度、長時間內事件的發生頻率等等。《牛津英語辭典》裡提供了另一個釋義是,「一句陳述或一個事件按照現有證據為真或成真的可能性。」碰上琳達問題的人知道,「長時間內事件的發生頻率」與主題無關,因為琳達是獨一無二的個體,重點在於她到底是不是一個女權主義者銀行行員。正常對話裡,講者提供生理特徵多半帶有動機,希望聽者得出有意義的結論。心理學家雷夫. 赫維希(Ralph Hertwig)、 格爾德.吉格亨澤(Gerd Gigerenzer)表示:或許人類在琳達問題的情境裡,自然而然察覺此處的「機率」不應著重在數學層面的合取原則,而是非數學的「現有證據強度」,並基於證據做出合理判斷。
從這個角度出發,以特沃斯基和康納曼為首,學界做出新一波研究,結論發現只要引導受試者從相對頻率去思考問題,不放任心智困在何謂機率的思維泥沼,就比較容易重拾合取原則。想像世界上有一千個背景類似琳達的女性,請問其中銀行行員可能有幾位?投身女權運動的銀行行員又可能有幾位?這麼問的話,腦袋裡的小人沉默了,理智掙脫束縛,合取謬誤的比例大幅下降。
那麼合取謬誤作為機率概念不清的具體展現,難道只是文字曖昧誤導的結果?特沃斯基和康納曼仍然不同意,他們指出:就算測試加入賭注,而且是金錢,許多人依舊犯下合取謬誤(事實證明,押在琳達是女權主義銀行行員的人多,押在琳達只是銀行員的人少)。此外,即使改變問題形式引導受試者思考頻率,明明可以在心中具體計算行員數量了,犯錯的比例還是不低。這個現象背後的成因是某些人會將兩個情境抽出來單獨看待,沒有擺在一起比較,無法意識到子集大於母集的荒謬之處。
康納曼進而觀察到:人類維護既定觀念時特別不理性。所以他倡議解決科學議題的新方法,取代過去學界總是靠正反雙方你一言我一語、來來往往反反覆覆才論辯出少許進度。在「對抗式協作」(adversarial collaboration)中,兩邊事前約定透過一次實證檢驗解決爭端,並邀請公正第三方進行評判。身先士卒,康納曼與赫維希聯手研究琳達問題,找了心理學家芭芭拉.梅勒斯(Barbara Mellers)當裁判,兩個研究團隊決定執行三次實驗,都採取頻率形式的提問(「假設有一百個琳達這樣的女性,請問其中有多少會是……?」),排除單獨個體造成的認知影響。最後三人共同撰寫論文指出:「我們原本就不認為這次實驗能徹底解決爭議,結果也的確沒發生奇蹟。」就結論而言,雙方達成的共識是—縱使以頻率形式呈現問題,人類還是傾向合取謬誤。然而若脈絡足夠清晰,也就是選項容易比較、用字遣詞不留灰色地帶,人類比較有機會擺脫思考誤區。
(本文為《理性:人類最有效的認知工具,讓我們做出更好的選擇,採取更正確的行動》部分書摘)
書籍資訊
書名:《理性:人類最有效的認知工具,讓我們做出更好的選擇,採取更正確的行動》 Rationality: What It Is, Why It Seems Scarce, Why It Matters
作者:Steven Pinker
出版:商周出版
日期:2022











 最新文章
最新文章 主題總覽
主題總覽 成為粉絲
成為粉絲 追蹤IG
追蹤IG 追蹤推特
追蹤推特 也有串串
也有串串 合作提案
合作提案